
英语原文共 4 页,剩余内容已隐藏,支付完成后下载完整资料
复杂网络的探索
当今社会网络深入人心,有时我们害怕它的力量,这并不是没有原因的。1996年10月,在俄勒冈,因为两条电源线的故障导致一连串的电路瘫痪。美国和加拿大的两个省停电11个小时,大约700万客户停电达16次。2000年5月,迄今为止最具破坏性的计算机病毒爱虫蠕虫在互联网上传播,并在全球范围内造成数十亿美元的损失。
同时,科学家们也在考虑网络的力量对我们的影响。经过调查,食品网、电力网、细胞代谢、WWW、互联网、神经网络、电话网络,引文网络,这些数据库现在很容易访问。此外,强大的计算机的可用性已经使它能够探测到它们的结构。但是到目前为止我们并没有专门的设施来对这些网络数以百万的节点进行全面的计算。
为什么网络解剖如此重要?因为结构总是影响函数。例如,社会网络的拓扑结构影响信息和疾病的传播,以及电网拓扑结构的鲁棒性和稳定性影响的输电的效率和安全性。
从这个角度看,复杂网络是对复杂系统研究的一个更广泛的运动的一部分。科学家已经打破了许多系统。他们认为他们知道大部分的元素和力量。接下来的任务是要将它们,至少在数学模型方面捕捉整个合奏的关键特性。
但是,网络本质上是很难理解的,下面为网络可能出现的副作用。
1、结构复杂:接线图可能是一个复杂的问题。
2、网络演进:接线图可以随时间变化。在万维网上,页面和链接创建和失去的每一分钟。
3,联系的多样性:节点之间的连接可以有方向和程度不同。在神经系统中的突触可以是强或弱,抑制或兴奋。
4、动态复杂度:节点可以是非线性动力系统。
5、并发症:各种并发症的影响。例如,电网的布局取决于它是如何发展的。在过去的几年中,网络演进影响拓扑结构。当耦合神经元反复多次重复,它们之间的连接就加强了,这是记忆和学习的基础。在这里节点动力学影响连接权重。
为了取得进展,不同的领域有抑制某些并发症的措施。例如,在非线性动力学,我们倾向于几何结构结构简单几乎相同耦合在一起的动力系统。此外,我们通常假定网络体系结构是静态的。这些简化让我们回避任何问题的结构复杂性和注意力集中在系统的潜在的强大动力。
如果我们现在把许多这样的系统结合在一起,可以看出他们之间会出现集体行为吗?答案是会,但是不多。但是因此我们可以提出一些粗略的概括了。许多这样的模式可以共存,特别是如果节点有竞争的相互作用。在这种情况下,网络可能会变得沮丧,并显示大量的本地稳定的平衡。这种复杂的静态行为被认为如同自旋眼镜,联想记忆神经网络和组合优化的互相组合。
在相反的极端,假设每个节点具有一个混沌吸引子。在这种情况下,耦合体系结构的影响已经出现了一些规则。众所周知,相同的混沌系统的网络可以同步,他们的不稳定的波动会导致空间不稳定性。我们正在进行同一混沌映射、格动力系统和元胞自动机网络的相关研究。这些系统已经被使用,主要是为探索时空混沌和最简单的数学设置模式形成的平台,而不是实际的物理系统的模型。
复杂网络体系结构
到目前为止,所有关于网络拓扑结构的讨论都是有规律可循的。这些简单的架构使我们能够专注于复杂的节点的非线性动力学所造成的结果,而对网络本身而言不用承担任何额外的复杂性。现在,我采取互补的方法,设置动力学,并转向更复杂的架构。一个自然的开端是在光谱的另一端从规则网络开始的,进行统计是完全随机的。
想象很多纽扣散落在地板上。随机选择2个按钮,并将它们与线程结合在一起。重复这个过程并且总是选择对随机的按钮。(如果你连接的线足够大,你可你很有可能选择已经被连接到的纽扣,这当然是可以的,它只是创造了连接按钮集群。)结果是一个物理的例子,一个随机图有n个节点和m的链接。现在,将一个纽扣从地面拿起来。如果与这个纽扣直接或者间接连接的纽扣多,会造成什么后果?结果是网络会受到很大影响,你可能把一个孤立的按钮或者连接很少的纽扣被拿起来牵动的纽扣就会较少,复杂网络的节点和节点连接也是同样道理。
ERDouml;S和Reacute;nyi研究如何预期这种随机图的拓扑变化。M较小时,图形可能会分裂成许多小团簇的节点,称为组件。随着m的增加,构件增长,这些孤立的节点或小团簇会慢慢连接。相变发生在m= n/ 2,其中许多集群交联的自发形成一个巨大的组件。m>n / 2,这个巨大的组件包含n个节点的顺序,而其最接近的竞争对手只包含log n节点。此外,所有的节点中的巨型组件连接到每个其他的短路径:任何2个节点之间的最大程度的分离,增长缓慢,如log n。
随着这几十年的开拓性工作进行,随机图已经不光单纯在数学领域进项研究。他们还担任了基因网络的动力学模型理想化的耦合结构,生态系统和传染病和计算机病毒的传播等。
随机网络中的标度的涌现
Albert-Laszlo Barabasi;Reka Albert
科学;1999年10月15日,286年,5439;学术研究图书馆pg .509
系统的多样性,如遗传网络或万维网可描述为网络与复杂的拓扑结构。许多大型网络的共同特性是连通的顶点遵循幂律分布。此功能被发现是因为两个通用的机制:(Ⅰ)网络增长性和(Ⅱ)网络优先连接特性。这两个机制的连接导致了无标度网络的幂率特性。基于这两种成分的模型再现所观察到的静止的无标度分布,这表明大型网络的发展有强大的自组织现象,可以超越具体的个人系统。
当代科学不能描述具有多样化的非局域相互作用在许多学科的进展,例如分子生物学和计算机科学(1)。描述这些系统的困难在于它们的拓扑结构,其中许多形式的复杂网络的顶点是系统的元素,其边缘代表它们之间的相互作用。例如,在系统中形成一个巨大的遗传网络的顶点是蛋白质和基因之间的化学相互作用(2)。在不同的组织层次,一个大型网络是由神经系统构成的,其顶点是神经细胞,连接轴突(5)。但同样复杂的网络出现在社会科学中,顶点是个人或组织,边缘是它们之间的社会互动(4),或在万维网(WWW)中,它的顶点是HTML文档的链接从一个页面到另一个连接(5,6)。由于其庞大的规模和复杂性加之它们之间的多种多样相互作用,这些网络的拓扑结构在很大程度上是未知的。
传统上,复杂拓扑结构的网络已由Erdos和Renyi随机图理论描述(ER)(7),但在大型网络中数据的情况下,对这两个理论的预测在现实世界中很少经过实际测试。然而,由于数据采集的计算机化的推动,这种拓扑信息的可用性日益提高,提高了理解大型网络的动力学和拓扑稳定性的可能性。
在这里,我们的报告说明了已存在的高度的自组织特征的大型复杂网络的性能。探索了几个大型数据库描述网络拓扑结构,大跨度等不同领域的科学的WWW网或引用模式,我们表明,独立的系统和其成分的身份,概率P(k)代表网络中的顶点与其它顶点k相互作用衰变为一个幂律,以下以P(K)表明大型网络自组织成一个无标度特征的复杂网络时链接度为k的节点出现的概率,或者说一个新加入的节点连接到链接度为k的节点的概率,所有已知网络都存在不可预知的随机网络模型。我们发现,现有的网络模型未能纳入增长和优先连接,实现两个关键特征!网络可以使用一个模型结合这些成分,我们的模拟实验结果表明,他们是在现实网络中观察到的幂律缩放。最后,我们认为,这些成分在许多复杂的系统都会出现,这意味着我们的结果是相关的一大类网络观察到的性质,在形成一个很容易识别和重要的作用。
虽然有许多系统在形成复杂的网络时会有详细的拓扑数据.例如,几个电影演员的协作图代表了一个社会网络中的一个记录的例子。每个演员都有一个顶点,如果他们在同一个电影中被投在一起的话,他们就有两个演员在一起了小世界现象是某些复杂的特征网络,其中任意两个节点可以使用一些链接连接。这意味着两个节点之间的平均距离(即特征长度)是比较小的小世界。
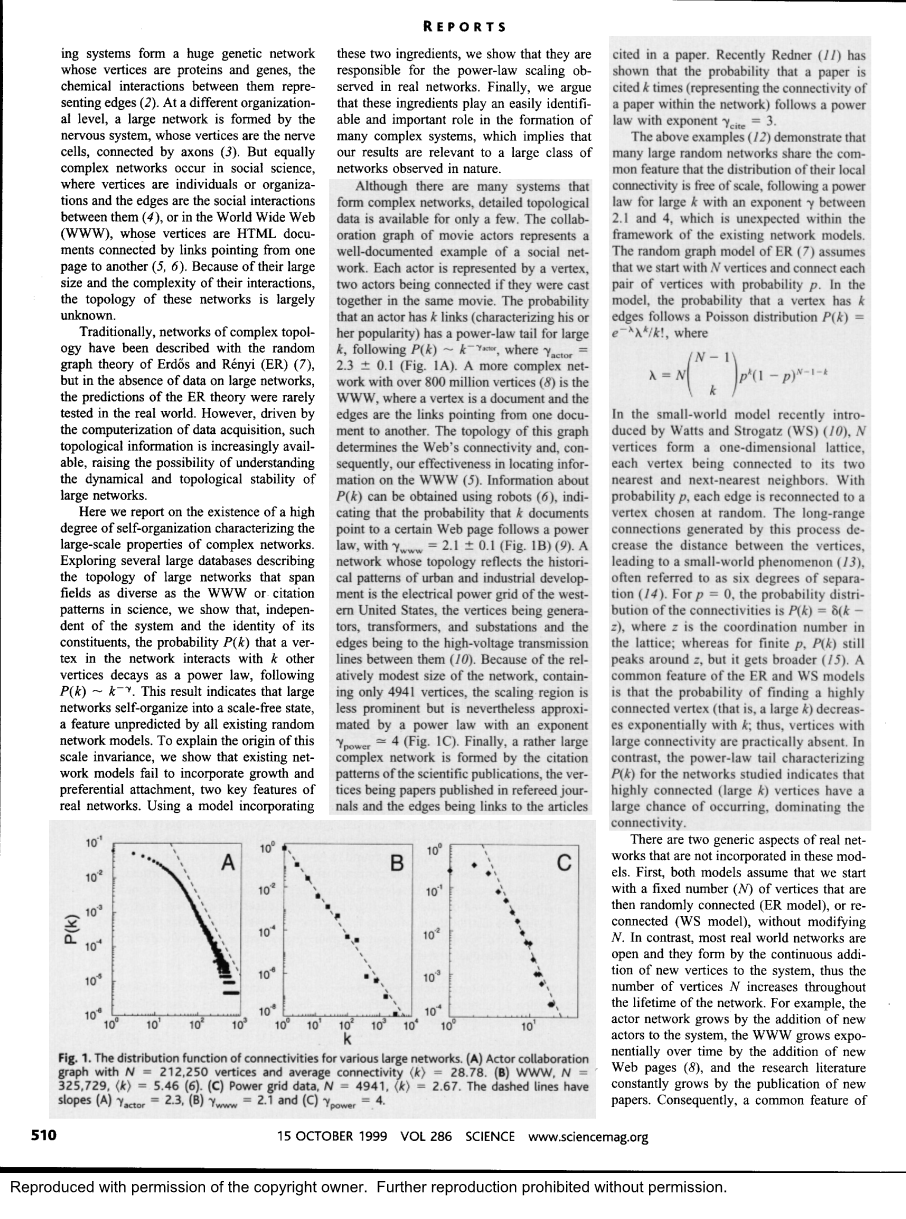
上面的例子(12)表明,许多大的随机网络共享的共同特征,他们的本地连接的分布是免费的规模,在和2.1之间的指数为7和4,这是意想不到的框架内,现有的网络模型的幂律。在小世界模型是最近由Watts和Strogatz(WS)(10),n个顶点构成的一维晶格,每个顶点连接它的两个近邻和次近邻。以概率p,每边连接到一个随机选择的顶点。远程连接所产生的这一过程中减少顶点之间的距离,导致小世界现象(J3),通常称为六度分离(14)。
对ER和WS模型的一个共同特点是,找到一个高度连接的顶点的概率很小,大连接顶点几乎是不存在的。
在这些模型中不包含实际网络的通用方面。首先,两模型的假设,我们从一个固定的数(AR)的顶点,然后随机连接(ER模型),或重新连接(WS模型),而无需修改的,相反,大多数现实世界的网络是开放的,它们形成的新的顶点的连续体系之外,因此顶点增加网络的整个生命周期的数量。例如,行动者网络增加新的演员加入到系统,WWW呈指数增长,随着时间的推移,新的网页添加,研究文献的不断增长的新论文的出版。因此,一个共同的特点ofhese系统是网络不断扩展到新的顶点连接系统中已有的顶点添加。
其次,随机网络模型假设2个顶点连接的概率是随机的,均匀的。相比之下,最真实的网络表现出优惠的连接。例如,一个新的演员是最有可能被投在一个支持的作用更建立和更好的已知的演员。因此,一个新的演员将投以建立一个新的演员的概率是远远高于新的演员将演员与其他不太知名的演员。同样,一个新创建的网页将更可能包括链接到知名的流行的文件,已经很高的连接,和一个新的手稿更容易引用一个众所周知的,因此引纸比其引用的少,因此不太出名的同行。这些例子表明,一个新的顶点连接到现有的顶点的概率是不统一的,有一个更高的概率,它将被链接到一个顶点,已经有大量的连接。
在我们下一个模型的基础上,这些成分自然会导致所观察到的尺度不变分布。将网络的生长特性,从一个小的数(M0)的顶点,在每一个时间步,我们添加一个新的顶点与M(SW0)边缘连接新的顶点到顶点w。不同系统中已有的,要结合优先连接,我们假设一个新的顶点的概率将被连接到顶点/取决于连接度。
随机网络模型导致自然出现的不平衡性。这个网络发展成一个一个顶点有k条边的概率尺度不变的状态,因为真实的网络观察电源法描述了在其发展的不同阶段而不同尺寸的系统,可以预期的是,正确的模型应该提供一个分布的主要特点是独立的时间。事实上,如图2a显示,P(k)是独立的时间(和随后的独立的系统的大小),表明尽管不断增长,系统组织成一个无标度的静止状态。
由于优先连接,一个顶点,获得更多的连接比另一个将增加其连通性在一个较高的速率,因此,2个顶点之间的连通性的初始差异将进一步增加,随着网络的增长。率在顶点获取边缘使K 。在TF的时候,顶点/添加到系统(图2C),缩放属性,可以直接测试一次时间分辨数据网络连接可用。年龄越大(小TT)顶点增加连接在年轻消费,经过一段时间导致一些顶点高度关联,在实际网络中,可以很容易地检测到的现象。此外,这个属性可以用来计算7个解析。这一点我有一个小于k连通概率,虽然它再现所观察到的无标度分布,该模型无法预期到网络的各个方面的研究。为了这个,我们需要更多的细节来模拟这些系统。例如,在模型中我们假定的线性择优;然而,虽然一般可以有任意的非线性形式IL(AR)~ KA,仿真结果表明,缩放是目前只有一个.此外,指数得到不同的网络分散2.1和4之间。然而,它是很容易修改我们的模型来解释指数不同的7=3。例如,如果我们假设一个分数的磷的链接是指向,这是支持的数值模拟(16)。最后,一些网络的发展不仅增加了新的顶点,但增加了建立顶点之间的连接(有时删除)。虽然这些和其他系统的具体功能可以修改的指数7,我们的模型提供了第一个成功的机制,占实际网络的规模不变的性质
增长和优惠的附件是一个复杂的系统,包括商业网络(17,18),社会网络(描述个人或组织),运输网络(19),等等。因此,我们期望在所有系统中,详细的数据已经可用的规模不变的状态,我们是一个通用的属性,许多复杂的网络,适用范围远远超出了引用的例子。一个更好的描述这些系统将有助于研究其他复杂的系统,这是目前较少的拓扑信息,包括重要的例子是遗传或生物系统中的信令网络。我们通常不认为生物系统是开放的或不断增长的,因为它们的特性是基因编码的。然而,遗传和信号网络的无标度特征可能能反映网络吗?进化史,主要是由不同成分的生长和聚集,导致从简单的分子到复杂的生物。在映射出遗传网络的快速发展,这些问题的答案可能不会太远。类似的机制可以解释执政竞争系统的社会和经济差距的根源,因为无标度的不均匀性是由于单个顶点的地方决定自组织的必然结果,在此基础上偏向更多可见的信息(富裕)的顶点,不论这种可见性的本质和起源。
参考文献
R. Gallagher and T. Appenzeller, Science 284, 79 (1999}; R. F. Service, ibid., p.
C. Wengl U. S. Bhalla, R. Iyengar, ibid., p. 80.
C. Koch and G. Laurent, ibid., p. 96.
S. Wasserman and K. Faust, Social Network Analysis (Cambridge Univ. Press, Cambridge, 1994).
Members of the Cfever project, Sc/. Am. 280, 54 (June 1999).
R. Albert, H. Jeong, A.-L. Barabasi, Nature 401, 130 (1999); A.-L. Barabasi, R. Albert, H. Jeong, Physica A 272, 173 (1999); see also
http://www.nd.edu/~net- works.
P. Erdos and A. Renyi, Pubi Math. I
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[147822],资料为PDF文档或Word文档,PDF文档可免费转换为Word


